▷ #TSCLab #TCLab #ESP32 #Arduino #Control #MACI
By: Ulbio Alejandro
En el siguiente blog se presenta la vigésima sextapráctica del laboratorio de control de temperatura y velocidad de un motor.
Objetivo general:
- Realizar la identificacion de sistemas, empleando datos anteriormente adquiridos de un Motor DC.
Materiales:
- Matlab
- TSC-Lab
Código de Matlab:
Introducción:
Es importante realizar una prueba en lazo abierto sobre la dinámica del sistema, el mismo que por medio de un Tren de pulsos podemos obtener los datos de la salida, los cuales resultaron la velocidad del motor DC en RPM. Para este ejercicio, se utiliza un archivo denominado OpenLoopMotorDC.csv el cual contiene tanto la entrada como la salida de la planta, cabe destacar que la entrada es un pulso unitario para experimentar la dinámica del sistema.
Ilustración 1 Variables de proceso del archivo tipo .csv
Mediante código de MATLAB, procedemos abrir el archivo para extraer los datos tanto la entrada como la salida. De esta forma obtenemos la respuesta del sistema para su posterior análisis.
Ilustración 2 Script de MATLAB.
Ilustración 3 Gráfica de los datos obtenidos en la prueba de lazo abierto.
En caso de que la planta lo amerite, es posible realizar un filtro para mejorar la respuesta del sistema, debido a que existen perturbaciones en la toma de datos donde es importante filtrar la señal para que la curva tenga un comportamiento más suave. Para ello, es importante tener el tiempo en estado estable de la curva que tenemos actualmente y luego encontrar los polos del filtro, el cual se especifica en el siguiente script.
Ilustración 4 Código para aplicar un filtro en la señal.
El polo que contempla la función de transferencia del filtro debe ser lo suficientemente alto para sin perder la dinámica del sistema y, lo suficientemente bajo para filtrar el ruido que presenta, teóricamente se indica que debe ser 5 veces el polo dominante encontrado, pero es posible ajustarlo mediante la simulación del filtro con el comando lsim().
Ilustración 5 Parte del código donde indica un filtro para la señal de control.
En este ejemplo, no se realizó dicho filtrado ya que se considera que el ruido presente cuando se adquiero los datos del lazo abierto es aceptable, sin embargo, se muestra el código en caso de que las circunstancias lo ameriten.
Es importante determinar el punto en el que la curva se estabiliza al momento de activar la señal de alto por medio del microcontrolador, como presente cierto ruido se realiza un promedio de todos los datos que se obtuvieron en el sistema, dando así un valor de 5742.4 [RPM].
Ilustración 6 Puntos de estado estable según la dinámica del sistema al aplicar un tren de pulso.
Luego, es posible encontrar el tiempo de estabilización de la curva, considerando que la respuesta es de primer orden, dando así Tss= 4[s] el cual se lo obtuvo por la banda del 2% alrededor del punto de estado estable. Cabe destacar, que en este caso el punto de operación de la salida es 0 [RPM] debido a que es el punto inicial donde parte la característica del lazo abierto, tal como se muestra en las figuras.
Ilustración 7 Obtención del tiempo en estado estable de la curva.
Es importante que al ingresar al Toolbox System Identification de MATLAB, tanto la entrada como la salida deben estar sin el punto de operación, es decir, se considera la variable incremental del proceso. En este caso, resulta que la variable completa es igual a la variable incremental y por ese motivo no se resta el punto de operación. Para abrir la aplicación se lo llama mediante el siguiente comando:
Ilustración 8 Comando para inicializar el Toolbox.
Luego, el aplicativo se muestra como en la siguiente imagen.
Ilustración 9 Primera vista del Toolbox System Identification.
El toolbox de MATLAB resulta ser intuitivo, donde por medio de flechas es posible guiarnos la secuencia de pasos a realizar para obtener una representación matemática de la planta de control (Motor DC). En primera instancia, se debe importar los datos, el mismo que debemos seleccionarlo con el nombre Time domain data tal como se muestra a continuación:
Ilustración 10 Opción para ingresar los datos al toolbox.
Tanto la entrada como la salida son los datos trabajados en el workspace sin el punto de operación previamente en el script, lo que se hace son llamarlos por el nombre de las variables correspondientes. Es posible dar un nombre a los datos en Data name, además de colocarle el tiempo inicial que es 0 y el tiempo de muestreo, que para este ejercicio se lo ha realizado como 1 segundo por muestra (este parámetro es importante, se debe establecer al momento de realizar la adquisición de datos de su planta de control). Una vez ajustado todos los parámetros, se da clic en Import.
Ilustración 11 Establecer los datos en el Toolbox.
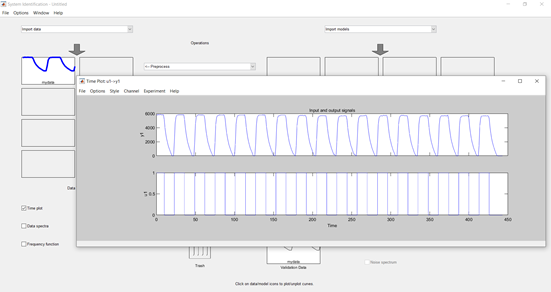
Para observar que los datos fueron extraídos del Workspace del script, es posible dar clic en Time plot, el mismo que se encuentra en la parte inferior derecha del Toolbox. Además, se encuentra establecido por el nombre previamente escogido. Time plot permite graficar todos los datos que se encuentren en los cuadros del lateral izquierdo, en caso de tener más de una gráfica es posible segmentarla solo dando clic a los cuadros que necesitaremos visualizar.
Ilustración 12 Uso del Time plot para visualizar los datos en el Toolbox.
Es importante establecer los datos un rango de trabajo, ya que existen parte de la curva que no son considerados en el análisis. Para esto, se debe ir a una venta de interacción y seleccionar Select range, tal como se muestra en la siguiente imagen.
Ilustración 13 Selección de un rango de toda la curva en el Toolbox.
El criterio utilizado para seleccionar los rangos de la curva es destacar aquellas gráficas que no son similares al resto, además de segmentar las regiones de trabajo. Para esto, en esta ocasión se considera el criterio de: 70% de toda la señal servirá como entrenamiento de la identificación de sistemas, mientras que el 30% restante de la señal será como validación de los datos. En la gráfica, se puede observar 16 respuestas al activar un flanco alto en la adquisición de datos, obteniendo el 70% se consideró que alrededor de 11 primeros pulsos son para entramiento, mientras el restante es para validación.
Ilustración 14 Selección del 70 % de la curva, entrenamiento.
Ilustración 15 Selección del 30% de la señal, validación.
Cada vez que se seleccione la opción Insert, todas las curvas se irán generando en la vista de los datos, donde por medio del Time plot podemos observar la sección de las curvas seleccionadas.
Ilustración 16 Se muestra los datos que serán para entrenamiento.
Ilustración 17 Se muestra los datos que serán para validación.
✅ Método 1
Luego, debemos arrastrar los datos respectivos tanto en el Working Data (70% de la señal) y Validation Data (30% de la señal), para comenzar a estimar el modelo matemático que simulará el sistema en cuestión, esto se realiza seleccionando Process Models.
Ilustración 18 Selección del Process Model.
Luego, aparecerá una ventana donde podemos estimar las distintas opciones o funciones de transferencias disponibles en el Toolbox, las mismas que serán en consideración del programador. Entre ella tenemos la función de transferencia con cierta cantidad de polos desde el 0 hasta 3, luego de que sean raíces reales o complejas conjugadas. Es posible realizar las variaciones que considere el usuario, una vez seleccionado cuales son las variantes que se desea, se debe dar clic en Estimate.
Ilustración 19 Selección de la función de transferencia a modelar el sistema.
Todos los modelos matemáticos obtenidos serán guardados en los recuerdos del lateral derecho, los mismos que tendrán distintos nombres y colores para que el usuario pueda identificarlos fácilmente.
Ilustración 20 Ajustando las características de un nuevo modelo matemático.
Ilustración 21 Obtención de todos los modelos matemáticos considerados para esta práctica.
Una vez obtenido todos los modelos que Matlab pudo simular a partir de los datos proporcionados, es posible compararlos y medirlos con la salida. Para esto, se debe dar clic en el recuadro inferior derecha denominado Model Output, el mismo que mostrará lo siguiente:
Ilustración 22 Clic en Model Output para acceder a la comparación de los modelos.
Luego, se obtiene una comparación entre los datos de la validación antes ajustados en el Toolbox, los mismos que serán modelados de acuerdo con el ajuste matemático escogido. En la parte derecha podemos visualizar el porcentaje de ajuste correspondiente a las señales de la izquierda y dependiendo de la estructura de la función de transferencia simulada. Para esto tomamos los siguientes criterios para destacar cada modelo:
- Se debe tener un porcentaje de ajuste mayor al 70%, los que simbolicen menor al mismo serán descartados inmediatamente.
- Se debe tener en consideración el tipo de función de transferencia a escoger, esto indica que sea lo más simple posible para realizar el modelado de esta.
En un caso hipotético que tengamos que escoger entre una función de primer orden con un ajuste del 89% y una función con polos conjugados complejos con un ajuste del 95%, muy probablemente se selecciones la primera función debido a la facilidad de análisis que conservar los de ese tipo de funciones de transferencia.
Ilustración 23 Porcentaje de ajuste de los distintos modelos encontrados.
✅ Método 2
Otra forma de realizar los pasos anteriores es dando la opción de Transfer Function Models, el mismo que ayudará ajustar los distintos modelos matemáticos para llegar al mejor porcentaje de ajuste posible.
Ilustración 24 Selección del segundo método para encontrar la representación matemática adecuada.
Luego, debemos indicarle cuales son las características que deseamos comparar entre los distintos modelos matemáticos que nos ofrece el Toolbox.
Ilustración 25 Ajuste de los parámetros.
Luego estimamos, para poder encontrar la mejor representación matemática posible. En este punto se da como recomendación tener varias opciones para estimar el mejor resultado según los criterios antes mencionados.
Ilustración 26 Primera Estimación del modelo matemático en el Toolbox.
Ilustración 27 Segunda estimación del modelo matemático en el Toolbox.
Ilustración 28 Tercera estimación del modelo matemático en el Toolbox.
Una vez que se haya seleccionado el mejor modelo matemático, es posible exportar la función de transferencia, arrastrándolo con el mouse y llevándolo en la opción To Workspace.
Ilustración 29 Enviando al Workspace la Función de transferencia resultante.
En este ejemplo se tienen las dos funciones de transferencia escogidas, pero solo nos servirá una y es la que se denomina como tf1, debido a que resulta mucho más simple que tf2, tal como se muestra en la siguiente imagen:
Ilustración 30 Funciones de transferencia resultantes.
✅ Método 3
Otra forma rápida de como obtener un modelo para la identificación de sistemas es usando el estimador Quick Start.
Dar click derecho sobre el modelo seleccionado en la venta System Identification y se despliega la ventana Data model info:
Dar click en Export para exportar el modelo a Matlab.
En la parte final del código de matlab está la forma de presentar la función de transferencia de forma polinomial para facilitar su ingreso en el Simulink.
✅ Test Identification Model
Finalmente, se propone emplear el siguiente simulink para comprobar la similitud entre la planata real de motor en el TSCLAB y el modelo identificado.
Simulink:
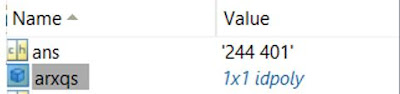
Comments
Post a Comment